Immer wieder werden die Spikes von Newton-Teleskopen thematisiert. Manche Leute mögen sie, viele nicht und es ist nun mal Tatsache, dass eine Dreiarm-Spinne an Sternen sechs, eine Vierarm-Spinne vier Spikes erzeugt. Visuell sieht man das an hellen Sternen. Die Lichtbeugung erzeugt helle, schmale Strahlen und natürlich haben solche Spinnenbeine, so schmal sie auch sein mögen, eine Länge und Fläche. Je größer sie sind, um so mehr Beugungserscheinungen, um so heller und länger sind die Spikes an einem Stern definierter Helligkeit. Ganz Spitzfindige ziehen auch noch die Fläche der Spinnenbeine von der lichtsammelnden Fläche ab, da sie ja einen Teil des Hauptspiegels verdeckt.


In Diskussionen die solche Wendungen nehmen wird dann schon mal eine gebogene Spinne, englisch "curved spider", erwähnt, da hier die Beugungserscheinungen zwar nicht vermieden, aber eben, gemäß der Krümmung der das Licht beugenden Kanten, ins Feld gestreut werden. Es entstehen keine Spikes auch helle Sterne bleiben rund. Als Gegenargument wird dann gebetsmühlenartig dargelegt, dass ein Lichthof um das Objekt gestreut wird und dass sogar mehr Beugungserscheinungen und Lichtverluste entstehen, da eine ausreichend steife und justierstabile gebogene Spinne grundsätzlich mehr Länge habe und dicker sein müsse als eine übliche Spinne mit geraden Armen, also auch auf mehr Fläche komme.
Dem bin ich dann mal auf den Grund gegangen, aber zuvor muss noch geklärt sein, für wen und für welche Newtons-/Dobsons sich ein Umbau überhaupt lohnt.
Geeignet sind z.B. stabile Volltuben von 4-10 Zöllern aus Hartpapier oder Alu, auch entsprechend steife Hüte von Gitterrohrkonstruktionen. Walzblechtuben bis 8 Zoll Öffnung, wenn das Blech nicht allzu dünn ist und die Tubusabschlussringe aus Metall sind, wie z.B. die Alugussringe von Skywatcher und GSO. Dünnblechdosen mit Bandmetall-Zierringen oder gar Plastikringen als Tubusabschluss sind denkbar ungeeignet, denn hier sorgt die, hoffentlich vorhandene, spannbare Fangspiegelspinne aus Metall dafür, dass der Tubus wenigstens halbwegs stabilisiert werden kann und somit die Justage im Gebrauch einigermaßen erhalten bleibt.
Ab etwa 6 Zoll Öffnung sollte das Teleskop visuell ausgelegt sein, also einen angemessen kleinen und damit eben im Verhältnis leichten Fangspiegel haben. Je mehr Gewicht an der Spinne hängt, um so verwindungssteifer muss die gebogene Spinne sein, was fast zwangsweise zur Verwendung dickerer Streben führt.
Wer fotografiert, also Licht über Zeit sammelt und die Bilder nachbearbeitet ist mit einer dicken, in jeder Tubusdrehung justierstabilen Vierarmspinne sehr gut aufgestellt, da kann man sogar die weiter unten besprochenen "Apodisierungesmaßnahmen" andenken, aber hier geht es ums Visuelle am Dobson, die "Augenblickswahrnehmung" und daher so wenig sichtbare Beugungserscheinungen wie irgend möglich.
Okay, wie sieht es denn nun in der Praxis aus? Ich persönlich beschränke den Einsatz von gebogenen Fangspiegelspinnen auf maximal 8 Zoll Öffnung und visuelle Auslegung. Also ein Tubusinnenmaß von 230 bis 240 mm und ungefasste Fangspiegel unter 60 mm kleine Achse. Ich zeige hier meinen 6-Zöller, der 12-Zöller nebendran bleibt wie er ist.


Die Perspektive täuscht etwas durch den deutlich längeren Tubusüberhang des 6-Zöllers und auch durch die doppelte Größe des 12-Zöllers. Also lohnt mal ein weing Nachrechnen und das machen wir mal anhand des gängigen 8 Zoll f/6 mit einem 50 mm Fangspiegel und 230 mm Tubusinnenmaß.
Radius= 115
Durchmesser: 230
Umfang: 722.566
Flächeninhalt: 41547.563
Eine Vierarmspinne ist nur in ihrem sichtbaren Bereich optisch wirksam, folglich wird der Radius des Fangspiegels (25 mm) von der Länge jedes der vier Spinnenbeine abgezogen. Es bleiben 4 x 90 mm, gleich 360 mm. Das steht einem Flächeninhalt des Hauptspiegels von 31416 mm gegenüber, der Fangspiegel kommt auf 1963 mm. Ich denke, die Zahlen sprechen für sich.
Rechnen wir mit dem durchaus üblichen Millimeter für die Dicke der Streben haben wir einen Flächeninhalt von 360 mm. Es gibt auch Spinnen mit 1,5 mm Strebendicke oder (seltener) 0,8 mm. Bei den Fernost-Newtons finden wir meistens 1 mm vor.
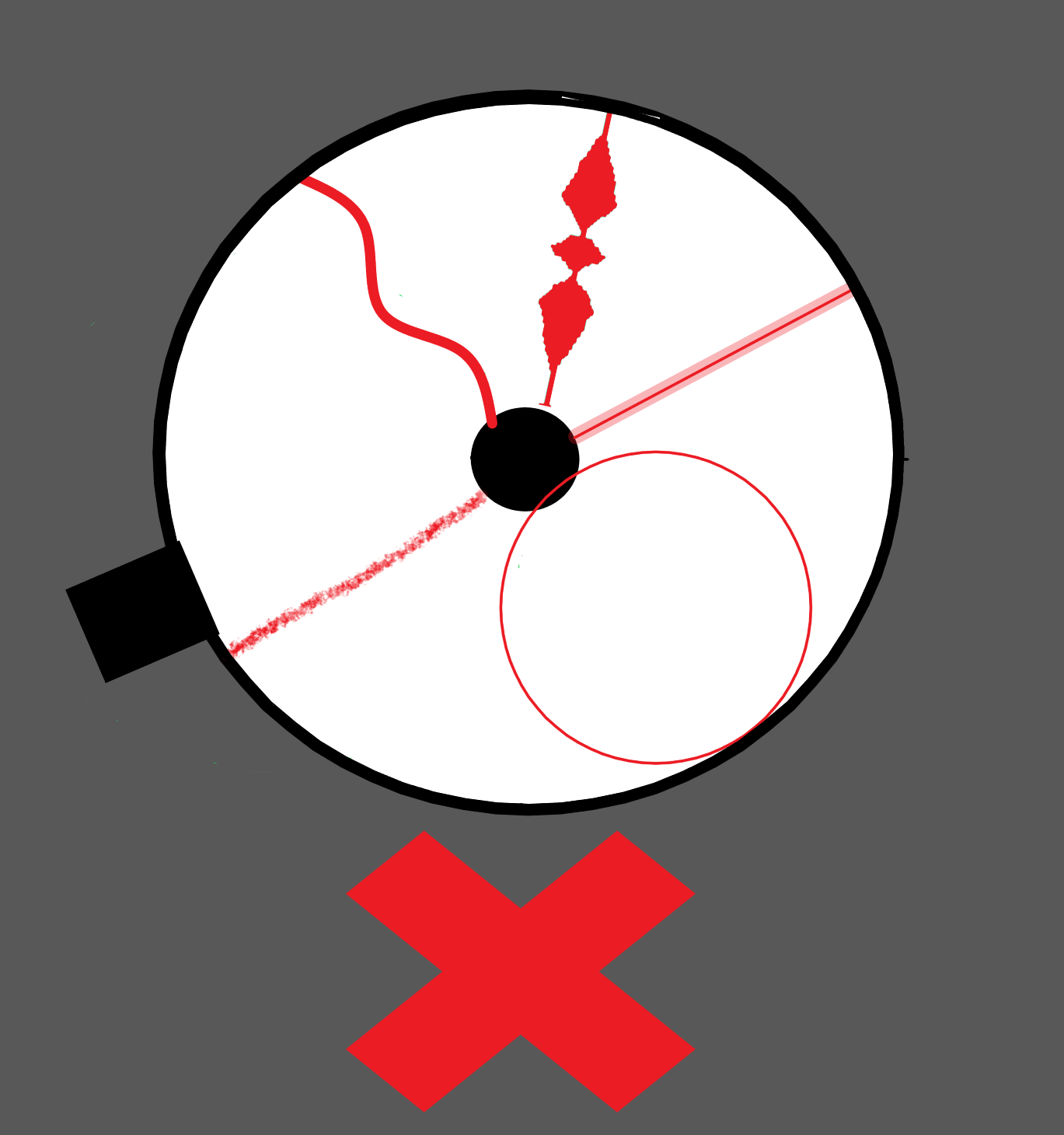
Meine gebogene Spinne, grün eingezeichnet, stellt im Tubus etwa die Hälfte eines kleinen Ovals mit 120mm Breite und 92,5 mm Länge dar. Das ist an der Okularauszugsbasis justierbar angebracht. Damit wird die Mitte des Teleskoptubus mit 185mm Durchmesser erreicht. Man kann auch, z.B. mit Drittelkreisen noch etwas sparen, ich habe das mal in der zweiten, nicht maßstäblichen Grafik rot eingezeichnet. Es gibt viele Möglichkeiten. Mir war die voll justierbare Anbringung an der Basis des Okularauszugs wichtig.
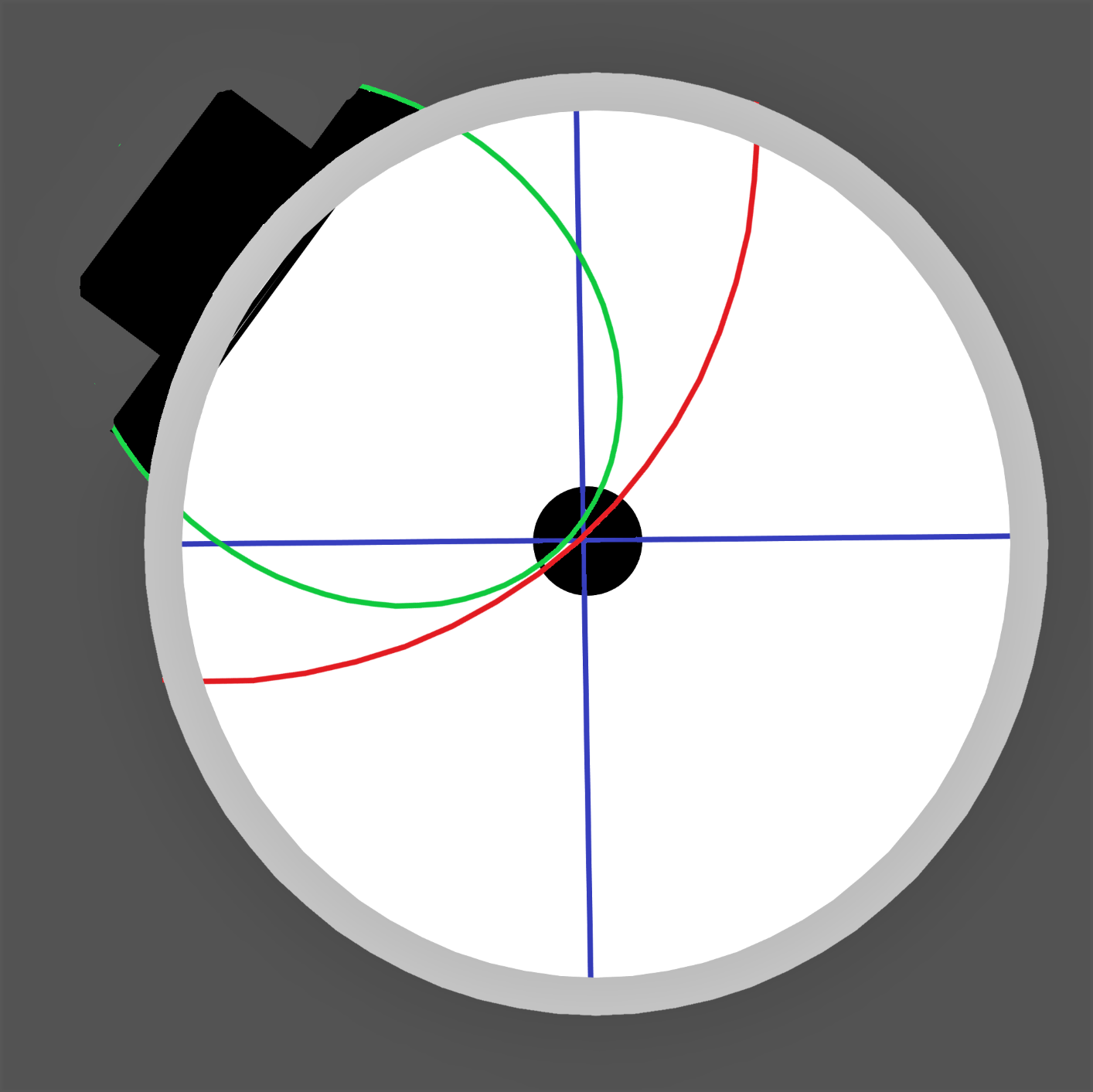
Für einen Newton sehe ich Konzepte mit drei bis vier gebogenen Armen, Doppelkreisen und was da noch alles unter gebogener Spinne zu sehen ist, absolut kritisch. Das ist unnötig und dann zieht das unausrottbare (Totschlag)Argument mit mehr Fläche und mehr Beugung durch mehr Kantenlänge natürlich, teilweise sogar krass. Wie sieht das aber hier aus?
Bei meinem 6-Zöller funktioniert ein, über den Tubus gezogener und so vorgebogener, Blechstreifen mit 1 mm Stärke und 30 mm Breite tadellos. Er wird mit deutlicher Spannung in den Tubus eingebracht, durch Schlitze im Tubus geführt und mit der OAZ-Basis verschraubt. Das Blech ist nicht dicker als die Streben der standardmäßig verbauten Spinnen mit geraden Armen. Allerdings ist das Schneiden etwas tricky, denn die Arme sind nicht nur vorgebogen, sie sind auch nicht gerade, sondern etwas V-förmig, um den Fangspiegel in der Mitte, zwischen den Armen zu positionieren. Der Schwerpunkt liegt dann auch etwa in der Mitte. Das vermeidet Verwindungen zum Schwerpunkt hin. Schlitze an jedem Ende dienen der Befestigung am Okularauszug und auch gleichzeitig der Justage des Systems durch Verstellmöglichkeiten in alle Richtungen. Der Fangspiegelhalter steckt einfach im Schlitz am oberen Ende des umgebogenen V und ist dort, in Neigung und Höhe, über Rändelschrauben verstellbar. Hat man dort ein mal die passende 45° Neigung eingestellt muss man da nie wieder ran. Die Nachjustage findet, wenn überhaupt mal nötig, immer über die Schrauben an der OAZ-Basis statt. Um eine Vorstellung davon zu vermitteln, hier mal ein altes Bild vom Rohzustand mit Fangspiegel und daneben die Befestigung am Okularauszug. So war die Lösung am alten 6 Zoll f/6.


Der Okularauszug am neuen 6 Zoll f/4,8 baut deutlich flacher und die Justiermechanik des Fangspiegelhalters, sowie dessen Rückseite hat eine Abdeckung erhalten. Tauprobleme am Fangspiegel waren im belüfteten Isotubus sehr selten, nun gibt es sie gar nicht mehr.




Das zwei Schrauben Prinzip ist auch mit je einem Schlitz im Blech, für zwei Schrauben an der Okularauszugsbasis, justierstabil. Es handelt sich um metrische Gewindeschrauben mit Gewindebuchsen im OAZ. Der Testlauf ist bestanden, ich muss mich nun mal an die Feinarbeiten machen. Ich werde an der Stelle auf Rändelschrauben verzichten und bei Kreuzschlitz bleiben. Da soll sich nichts ohne Werkzeug lockern und verstellen (lassen), das ist oft genug die (zu bequeme) Einladung zu unnötigem Handeln.
Die komplette Länge eines solchen gebogenen Teils im Tubus beträgt für einen 8-Zöller, den ich auch bei der Berechnung der Vierarmspinne gewählt hatte, etwa 250 mm, wovon wir sogar, eben wegen der Biegung, etwas mehr als 50 mm abziehen können die der Fangspiegel verdeckt. Egal, beim Flächeninhalt landen wir für diese gebogene Spinne bei etwas weniger als 200 mm, also runde 160 mm weniger als bei der Vierarmspinne. Wir unterhalten uns damit über Zweihundert bis Dreihundertsechzig von Einunddreißigtausendvierhundert Millimetern Fläche die zusätzliche Beugungserscheinungen einführen und Licht kosten. Wer den Lichtverlust und vor allem die, bei der geraden Spinne aus den Kanten resultierenden, Spikes an hellen Sternen nicht mag, verteilt das halt mit einer gebogenen Spinne in die Fläche des Bildfeldes. Was da in den Spikes, aufgrund der Konzentration auf einen ganz schmalen Lichtstachel, recht hell wirkt ist so gut wie nichts. Nimmt man z.B. einen 8 Zoll f/5 Newton mit einem 58 mm Fangspiegel in einer 1 mm dicken Fassung, erhöht das die zentrale Obstruktion um zwei Millimeter auf 60 mm und der Umfang beträgt dann 188 mm, der Zuwachs des Flächeninhalts 185 mm und ein entsprechend höherer Betrag an Licht fehlt und/oder wird in die Beugungsringe gestreut. Da bin ich mal gespannt, wer das sieht. Mit den 200 mm Flächeninhalt (m)einer gebogenen Spinne haben wir ein absolut vergleichbare Größenordnung die ins Feld gestreut wird. Das bleibt im visuell nicht nachweisbaren Bereich, da gibt es in der Praxis hunderte von Umständen von denen jeder hundertfach mehr Relevanz hat. Es bleibt lediglich eine rechnerische Übung.
Ich bin erster Mann auf der Baustelle, wenn es darum geht, unnötig hohe Obstruktionswerte kleiner zu machen und dabei noch die Ausleuchtung zu verbessern. Wenn ich ran gehe, dann will ich gerne von 35% auf 28% runter, wenn es geht auch von 28% auf 22%, aber für 2% von irgendwas lohnt das nicht. Für die Idee am Newton mal keine Spikes sehen zu wollen, kann das hingegen schon anders aussehen, aber da macht man doch besser den Rest, so weit als möglich, gleich mit. Darauf komme ich abschließend, anhand meines 6-Zöllers, nochmal zu sprechen.
Selbst eine Dreiarmspinne kommt nicht an eine sinnvoll gestaltete Curved Spider ran und dafür, dass man den einzelnen Spike etwas schwächer sieht, hat man sechs davon anstatt vier. Dem entsprechend kann also dann bei größeren Newtons, die mit einer gebogenen Spinne ausgestattet werden sollen, mit dickerem Material und/oder weniger Durchbiegung gearbeitet werden. Man könnte z.B. ohne mehr Beugungserscheinungen als mit einer 1 mm dicken Vierarm-Spinne zu erzeugen, 1,5 mm dickes Material verwenden und hätte dafür keine Spikes. Dem sind aber nach meiner Selbstbau-Erfahrung mit den günstigen Newton-/Dobsons aus fernöstlicher Produktion als Basis, irgendwann Grenzen gesetzt. Ich würde meinen 12-Zöller nicht selbst so ausstatten, während mich ein 8-Zöller noch reizt. Wer auf Heimwerkermittel angewiesen ist kann auf jeden Fall die für visuelle Beobachtung erforderliche Genauigkeit in Bearbeitung und Biegung erreichen. Für fotografischen Einsatz ist deutlich mehr Präzision gefragt, denn die Lichtsammlung über Zeit kann auch kleine Ungenauigkeiten, z.B. durch Lichtausbrüche und Refelxe, gnadenlos zeigen.
Kommerzielle, hochwertige Dobsons gibt es hingegen mit solchen Lösungen durchaus zu kaufen, z.B. von Taurus habe ich schon einen 18 Zoll Dobson mit einer gebogenen Spinne gesehen. Da gibt es wahlweise auch drei gerade Arme.
Es ist ja auch immer die Frage, warum man so etwas tut. Mich stören die paar Spikes an den hellsten Sternen visuell nicht, ich nehme sie während der Beobachtung gar nicht mehr wahr und nutze sie bei der Beurteilung der Justage am fokussierten hellen Stern, indem ich auf mögliche Langenunterschiede und Auffächerungen achte. Im Übrigen nimmt kaum jemand, auch kaum jemand von den versierten Beobachtern, die man auf den Wiesen schon mal antrifft, überhaupt wahr, dass mein 6-Zöller keine Spikes produziert, obwohl das unübersehbar ein Newton-Dobson ist.
Die gute Abbildung fällt, bei Erstbefassung, immer schnell auf.....sonst noch was.....öhhh...nee, was denn?
Hier nochmal eine schematische Darstellung der Justiermöglichkeiten, so wie ich sie bei meinen gebogenen Spinnen, die an der Basis der Okularauszüge befestigt werden, gelöst habe.
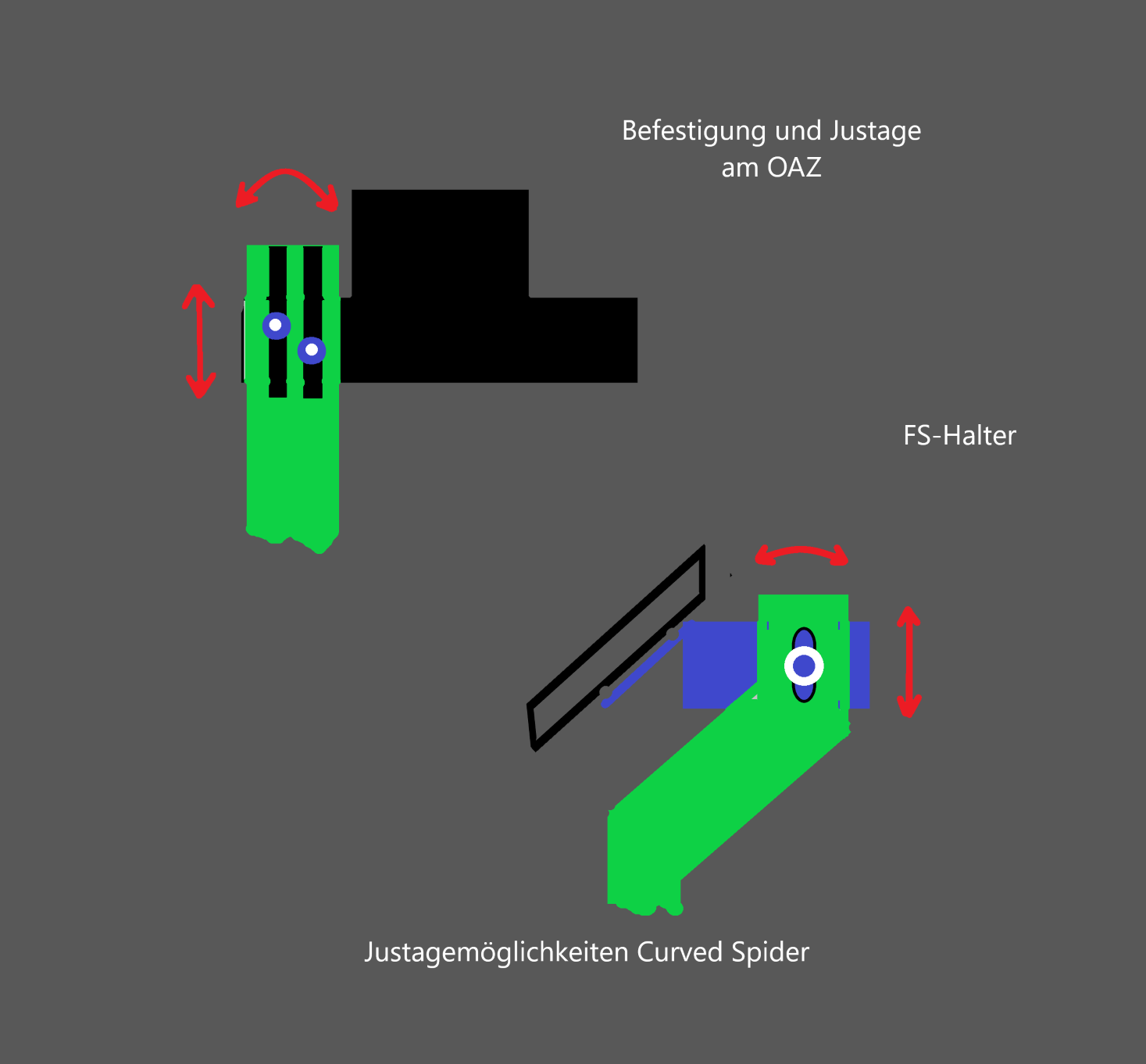
Bei einem Tubus für einen 8-Zöller kann das etwas knapp werden, dann kann man dort die Basis aufdoppeln oder löst die Befestigung und Justage unabhängig vom OAZ.
Die Einstellmöglichkeiten sind vielfältig, aber das ist so auch erforderlich. Die Spinne sollte dem Himmel halt schon nur ihre Schmalseite zeigen und nicht noch seitliche Fläche. Das kann man auch bei der gebogenen Spinne im Bild am defokussierten Stern gut sehen. Die Einstellung erfolgt am Fangspiegelhalter über den richtigen Kippwinkel und die passende Höhe. Eine gerade Spinne, deren Arme verdreht sind, fällt auch durch Doppel oder Fächerspikes am scharf gestellten Stern auf, das geht hier nicht. Mittenpositionierung und Feinjustage der Spinne erfolgen am Okularauszug. Die korrekte Ausrichtung des Hauptspiegels zum Fangspiegel erreicht man, wie sonst auch, anschließend über die Justierschrauben der Hauptspiegelzelle.
Eine sehr entscheidende Voraussetzung für einen guten Newton ist die korrekte Justage.
Nun ist so eine gebogene Spinne sehr schön, um mal einen Newton zu sehen, der keine Spikes an hellen Sternen produziert und die Spinne, richtig gebaut, kostet auch keinen Kontrast, weil sie eben nicht mehr, sondern eher weniger Beugungserscheinungen verursacht, Licht dto. Da mich persönlich die Spikes gar nicht stören war eher eine komplette visuelle Optimierung eines Newtons das Ziel und die gebogene Spinne passte halt ins Konzept.


Dieser Newton ist, mit dem 152/739er Hauptspiegel (f/4,8), dem nur 40 mm hoch bauenden Okularauszug und dem so möglichen 46er Fangspiegel nun immer noch nicht eben das, was gemeinhin als Planetenteleskop angesprochen wird, weil das immer noch 30% Obstruktion bedeutet und das Öffnungsverhältnis sehr groß ist. Noch dazu wird er auf Dobson-Montierung und meistens ohne EQ-Plattform betrieben. Er ist ja auch eigentlich eher auf Weitfeld ausgelegt. Da mich dann aber die sehr gute Leistung im mittleren und hohen Vergrößerungsbereich überzeugte, wurde er auch das bevorzugte Teleskop für meine Beobachtungen der Sonne im Weißlicht.
Man kann ihn in etwa mit den gängigen 150/750er Newtons vergleichen, die allerdings herstellerseits in aller Regel fotovisuell ausgelegt sind, also einen hohen Okularauszug plus Verlängerungshülse zum Erreichen des visuellen Fokus brauchen. Dem entsprechend benötigen sie einen überdimensionierten Fangspiegel. Sie kommen also auf, für visuelle Zwecke, unnötig hohe Obstruktionswerte. Mit dem üblichen, mindestens 70 mm hoch bauenden, Okularauszug plus mindestens 30 mm Verlängerungshülse zum Erreichen des visuellen Fokus kommt man mit einem 46 Millimeter Fangspiegel (der oft genug drin ist) bei der Ausleuchtung zu negativen Vorzeichen, verschenkt also Öffnung. Demnach muss man für ähnlich gute Ausleuchtungswerte den FS schon 10 mm größer nehmen. Auch wenn das jetzt alles grob überschlägig gerechnet ist, unter 35% Obstruktion geht dann, bei 150 mm Offnung und runden 750 mm Brennweite, nichts mehr.
Es sei denn man baut so ein Teil irgendwann doch mindestens so konsequent um wie ich. Mindestens, weil planetenlastig durchaus ein 42 mm Fangspiegel überlegenswert wäre und auf "Spitz und Knopf" gerechnet sogar ein 40er ausreichen würde. Allein, mir fehlt der Grund für die Anschaffung eines neuen, kleineren Fangspiegels, der ja belegbar ähnliche oder bessere Qualität als der vorhandene haben müsste, damit die Veränderung auch wirklich in die positive Richtung geht. Anstatt um den letzen Millimeter beim Fangspiegel zu feilschen verzichte ich lieber auf die üblichen drei bis fünf Haltebacken für den Hauptspiegel, deren großzügige Überdeckung der Verspiegelung ebenso selbstverständlich wie unnötig für zusätzliche Beugungserscheinungen sorgen und benutze einen Okularauszug, der nicht in den Strahlengang ragt, wie das vielfach üblich ist.



Bei solchen, keineswegs seltenen, absoluten Fehlkonstruktionen mit einem weit in den Strahlengang ragenden Okularauszugsrohr lohnt sich manchmal eine kleine Notoperation, wie ich sie im Artikel zu Filterschieber und Okularauszug schildere. Und die fetten Halteklammern, wie sie im mittleren Bild zu sehen sind, kann man recht einfach mit seitlichen Klammern die nicht auf den Spiegel drücken, sondern ihn mit einer dünnen Silikonwulst halten, vermeiden. Man sieht es eigentlich, doch man bedenkt es häufig nicht. Mit drei solcher Klammern wird mehr Spiegelfläche verdeckt als mit einer dünnen, geraden Fangspiegelspinne. Auch die sichtbaren Beugungserscheinungen können da mithalten, sind aber durch eckige Form und den Eingriff von außen nicht so markant wie der Lichtstachel eines Spikes. Sie sorgen eher für leichte Aufhellungen bis hin zu milchigen Halos um helle Objekte, setzen also den Kontrast herab. Das ist wiederum eine Eigenschaft, die man auch bei schlechten Spiegeln, also solchen mit niedrigen Strehwerten sieht. Ungemessen ist ein solcher Mangel des Spiegels schnell behauptet und ungeprüft auch schlecht zu widerlegen, aber so mancher verkannte Spiegel lief nach Entspannung, passender Lagerung und Befreiung von Klammern, nach Einbau einer Ringblende oder dem Umbau von massiven, dicken Fangspiegelstreben auf dünnere und/oder gar eine "curved Spider" sinnvoller Bauart, in einem optimierten Tubus schon zu großer Form auf.
Mein 6 Zoll Newton ist nunmehr mit dem 46er Fangspiegel absolut gesund so wie er ist, mit einem hellen, kontrastreichen, scharfen Bild bei Weitfeld und bei Sonne, Mond, Planeten gleichermaßen.

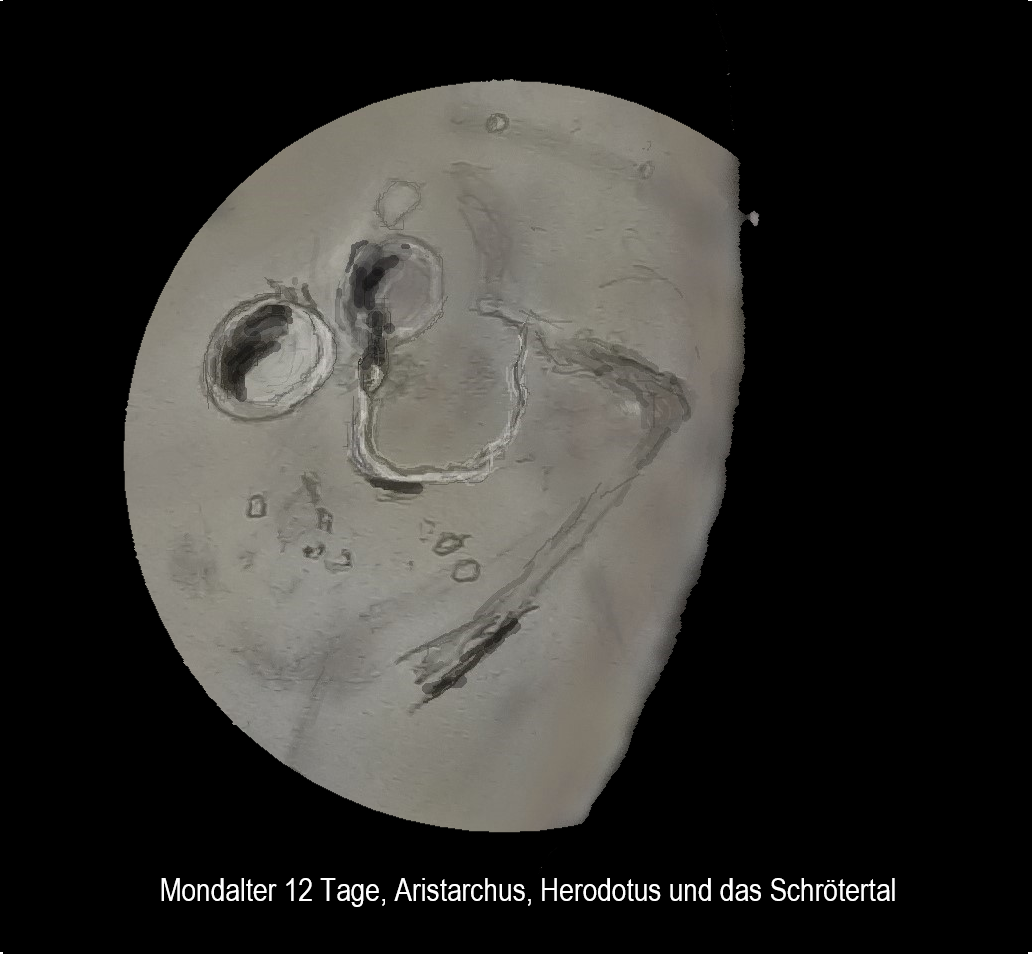
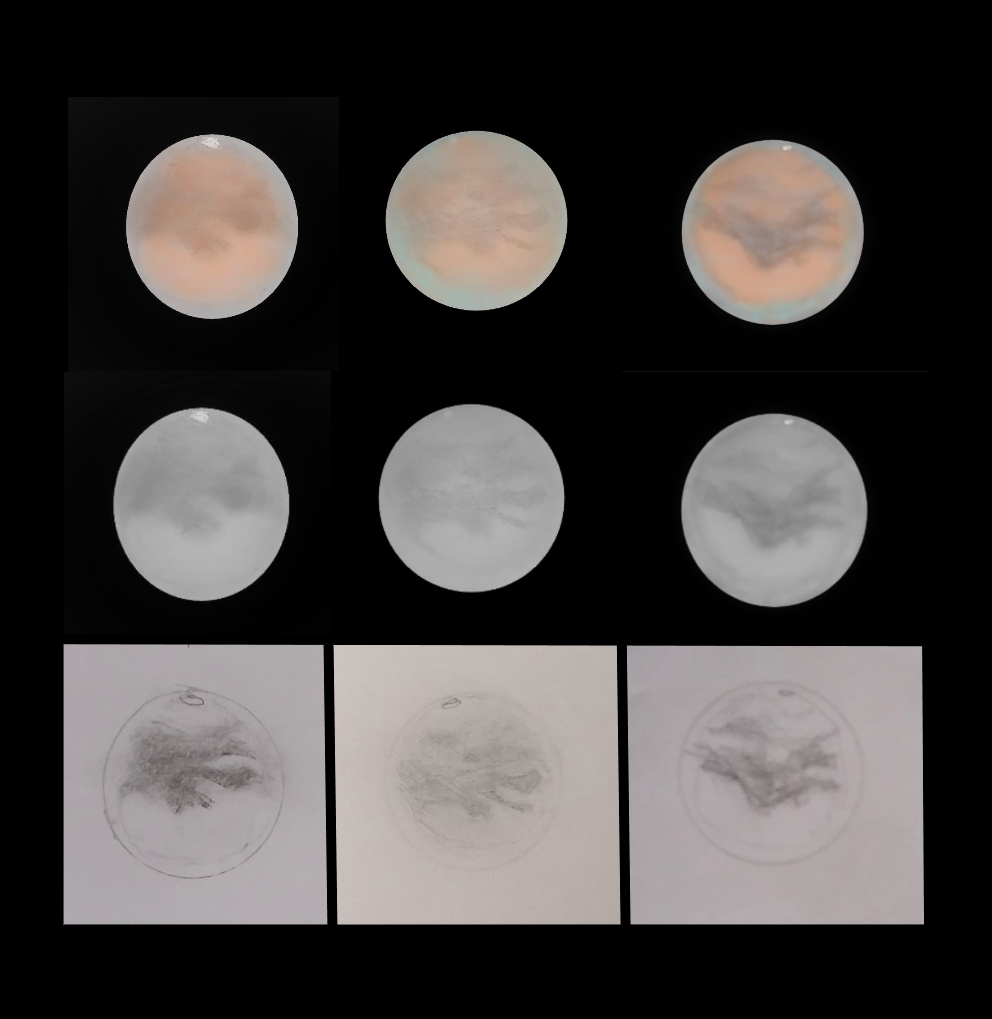
Mit solchen Ergebnissen kann ich sehr gut leben und das bleibt so.....bis mir ein günstiger 42er Fangspiegel mit einem glaubhaft und nachvollziehbar dokumentierten Zertifikat in die Hände fällt, das extrem hohe Planität der kompletten Fläche bis an die Kante und sehr geringe Oberflächenfehler ausweist. Das dürfte, nach bisher gemachten Erfahrungen, ein Weilchen dauern und ich bezweifele, dass meine Zeichenkunst ausreicht, um die, dann in Hoch- und Höchstvergrößerung zu erwartende, Verbesserung gut erfassbar zu dokumentieren.
Noch ein Wort zu so genannten Apodisations-Maßnahmen, die immer mal wieder in Debatten hochgekocht werden. Sie sollen Spiegelteleskopen die das nicht können sollen, zu einer APO-mäßigen Abbildung verhelfen und da haben in der kritischen Betrachtung natürlich Spikes einen sehr hohen Stellenwert.
So werden dann Fangspiegelarme mit Figuren maskiert oder selbst wellenförmig verbogen, andernfalls wird durch Veloursbeklebung ihre Dicke verdreifacht und die Spikes sind so gut wie weg. Wolle auf den Kanten geht auch und außerdem kaschiert/verhindert das die Sichtbarkeit der Kaltluft-Hülle um das zur Unterkühlung neigende Metall.
Man macht also aus zwei scharfen, schmalen Kanten viele breite Kanten mit Kurven, an Verdickungen auch mit nennenswerter Fläche, die in viele kleine Mini-Kanten zerstückelt sind. Die Beugungserscheinungen der vielen kleinen, ungerichteten, gebogenen Mini-Kanten werden nicht in scharfen Spikes gebündelt, sondern mehr oder weniger stark ins Feld gestreut.
In der Summe handelt man sich zwar zerstreute, doch auch deutlich mehr Beugungserscheinungen ein, da sie mindestens der Dicke (Fläche) der Streben mit dem Veloursmäntelchen oder der Dicke (Fläche) des Wollauftrags entsprechen. Wenn schon hinkende Vergleiche bemüht werden müssen, dann "apodisiert" das also tatsächlich nicht, das "achromatisiert" eher.
Die scharfen, dünnen Kanten einer sinnvoll konstruierten, gebogenen Spinne zerstreuen zuverlässiger, die Spinne hat zudem weniger Länge und damit weniger Fläche.
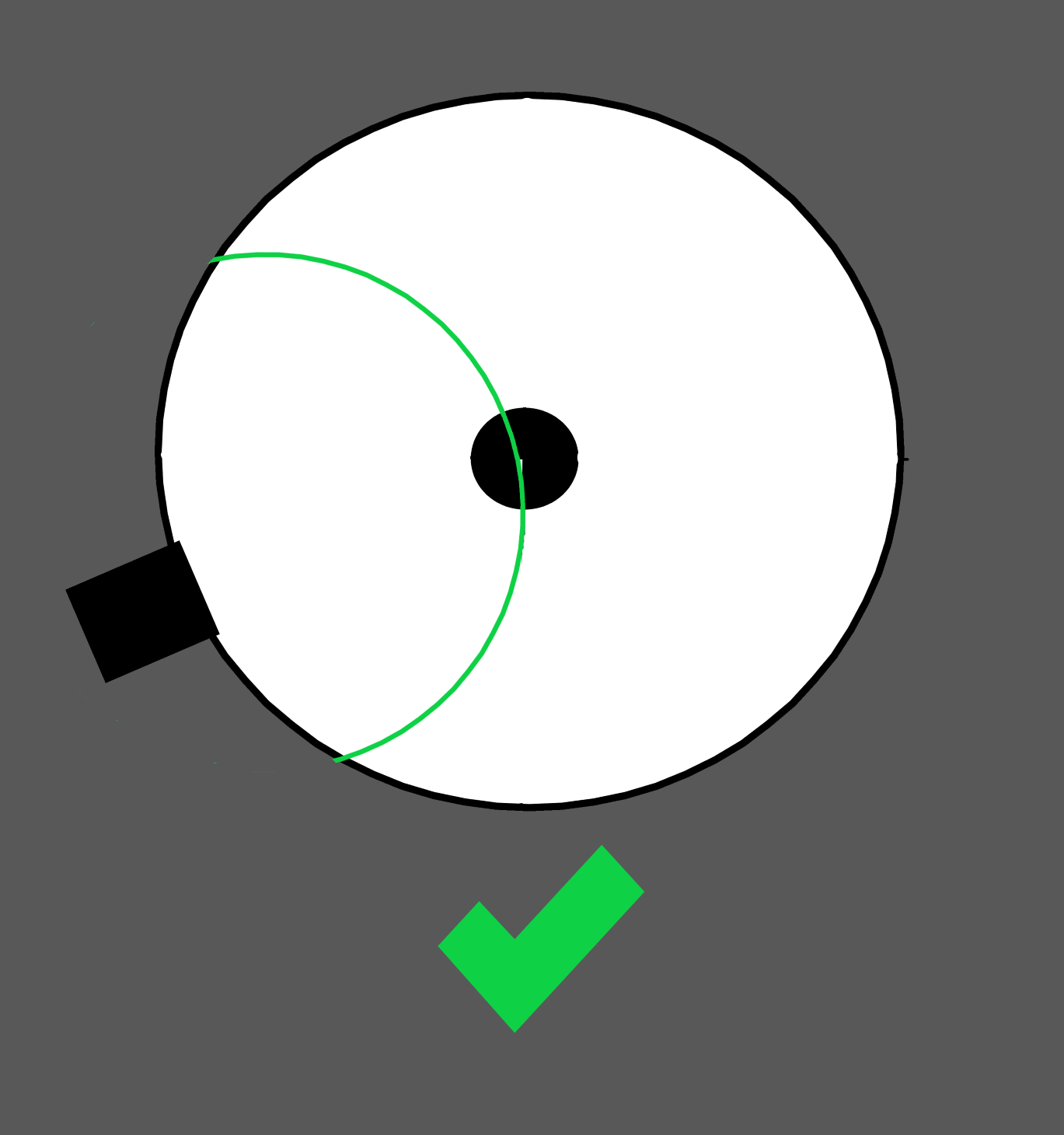
Oben der sinnvolle Weg zur vollständigen Vermeidung von Spikes nochmal in Grün, wobei die Biegung variabel ist, also stärker oder schwächer gewählt werden kann.
In Rot mehrere Wege die alle mehr Beugung einführen, egal ob ein Monoring, drei oder vier Wellen oder drei bis vier velours-/wollbeklebte gerade Arme und die barock anmutende Originalform der "Apodisierungsmaske".
Zufällig wurde ich Anfang 2022 noch auf eine interessante Variante der Diskussion in einem großen amerikanischen Forum aufmerksam, weil davon auch etwas in ein deutsches Forum schwappte. Es geht um das so genannte "Halszäpfchen", eine gebogene Einarmspinne, deren Form tatsächlich an das Zäpfchen erinnert. Das sieht erst mal aus, wie meine Halbkreisspinne gegenläufig zu geklappt, der Halter ist aber flächig ausgeführt.

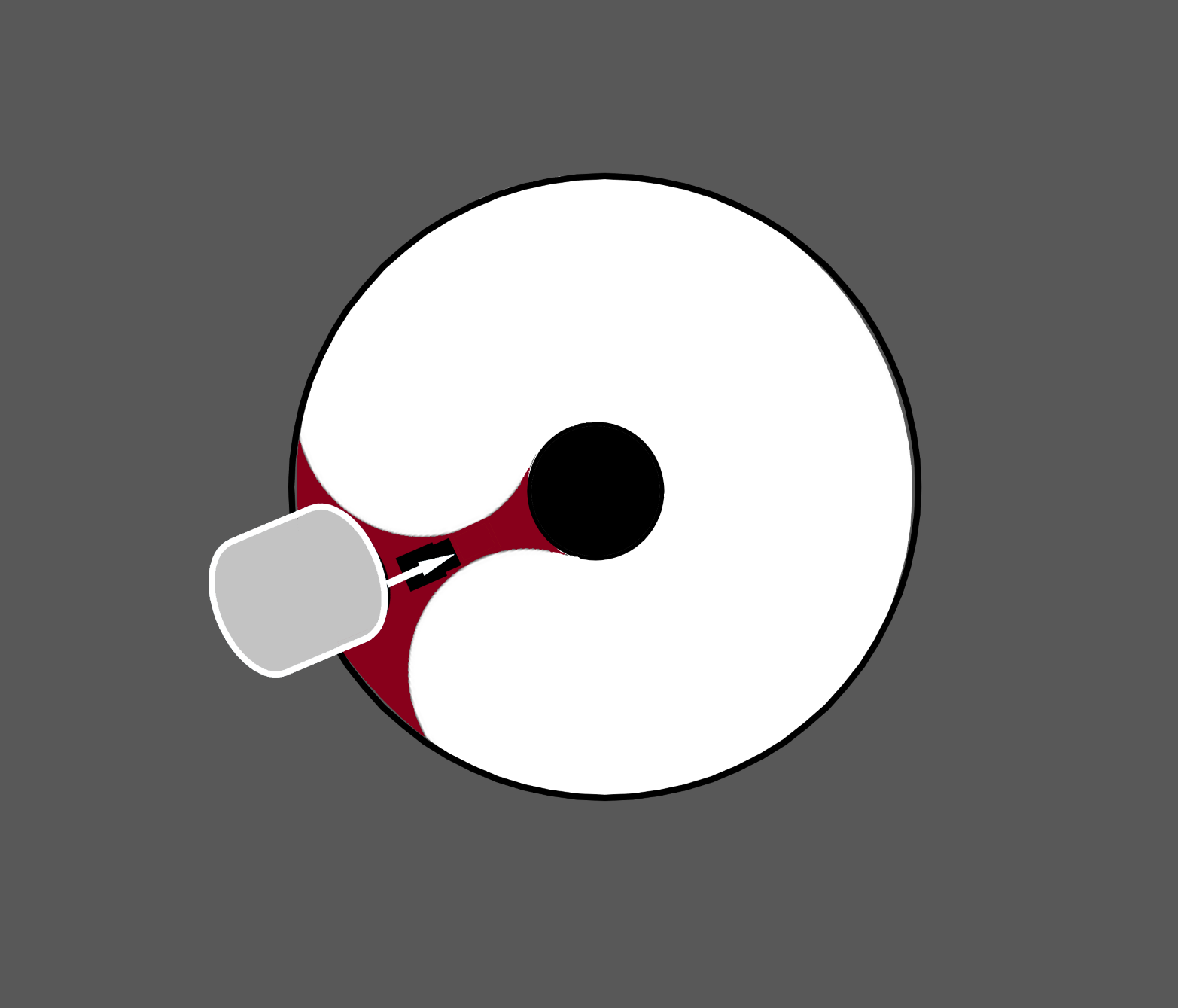
Okay soweit, gerade Kanten werden vermieden. Wir haben sogar nur zwei Außenkanten, da die Innenkanten aufgrund der Ausführung in Vollmaterial fehlen. Wie bei (m)einer Halbkreisspinne werden keine Spikes erzeugt. Während der Bügel der Halbkreisspinne allerdings selbst bei kleinen, ausgereizten Newtons, kaum mehr als 15% der Fläche des Fangspiegels hat und das bei größeren Newtons immer weniger wird, kommt man mit so einem Bügel im Minimum etwa auf die Fläche des Fangspiegels, eher mehr. Die Fläche der Obstruktion ist Lichtverlust im Zentrum des Beugungsscheibchens. Sie geht damit unmittelbar in die Helligkeit der Beugungserscheinungen ein, egal ob das in den Beugungsringen des Sterns an sich oder in hellen, gebündelten Spikes oder in der Verteilung auf die Fläche geschieht. Der Kontrast wird zwangsläufig schwächer. Die skalierten und normierten Simulationsbildchen aus Berechnungsprogramen, welche in den Foren gezeigt werden, geben wieder, dass dieses "Halszäpfcken" von Form und Ausprägung her Beugungserscheinungen wie eine gebogene Halbkreisspinne hervorruft.
Die massiv höhere Intensität durch deutlich größere Fläche lässt sich so wohl nicht darstellen, ist aber nun mal gegeben.
Dennoch kann so etwas interessant werden. Sehr große Dobsons (Newtons) brauchen sehr große Fangspiegel und das sind Planspiegel. Planspiegel in guter Qualität werden mit steigender Größe sehr schnell recht teuer und auch (mit allen Nachteilen die daran hängen) massig. Ist das Teleskop so groß, dass man einen 2-3 Zoll Okularauszug so innerhalb des Halszäpfchens näher am Hauptspiegel anbringen kann, dass er nicht in den Strahlengang ragt und eventuell sogar noch der Kopf des einblickenden Beobachters verdeckt wird, kann man einen deutlich kleineren Fangspiegel verwenden. Natürlich wird der Newton dem entsprechend länger, der Fokus liegt ja quasi im Tubus. Bei so einem Lowrider Dobson mit 50 bis 100 Zentimeter Hauptspiegel könnte der Strahlengang, je nach Brennweite, also passen. Zumindest könnte man das mal gegeneinander aufrechnen und schauen, was raus kommt.
Für den üblichen 6 bis 16 Zoll Dobson ist das aber eher nicht relevant.
Abschließend bleibt also festzustellen, dass sinnvoll konstruierte Drei- oder Vierarmspinnen visuell sichtbare Spikes an hellen Sternen erzeugen, auch wenn man die Streben dünn hält. Selbst bei sehr guten ATM-Spinnen aus 0,2 mm Bandstahl oder Drahtspinnen, die kaum noch Fläche einbringen, bleibt das so, weil es auf die Kanten ankommt. Will ich Spikes am Newton völlig ausschließen, ist eine gebogene Spinne (gebogene Kanten) mit möglichst kurzer Armlänge das Mittel der Wahl. Die Fläche ist, wie festgestellt, sehr klein, kleiner als bei den gängigen geraden Spinnen, ebenso die Länge der Kanten. Dem entsprechend sind auch unvermeidliche Beugungserscheinungen geringer, die ins Feld gestreut werden. Da gibt es, vom Seeing über die Himmelstransparenz bis zum Okular, deutlich schwerwiegendere Einflussfaktoren auf die Abbildungsleistung.
Nehmen wir doch nur mal den Hauptspiegel als ein Beispiel heraus. Bei den 8-Zöllern findet man Spiegel von 200 mm bis 205 mm Durchmesser als Herstellerangabe. Ich selbst habe einen Spiegel mit 198 mm Durchmesser von einem bekannten Hersteller liegen, der eigentlich 200 mm haben sollte. Wenn man da noch überall 2 mm für die Fase abzieht, ist von 7,7 Zoll bis 8 Zoll verspiegelter Fläche und das ist nun mal die Öffnung, alles vertreten. Darüber macht sich kaum jemand Gedanken. Das ist allerdings ziemlich genau der Unterschied an lichtsammelnder Fläche, der für den 50 mm Fangspiegel plus Spinne oftmals heiß diskutiert wird und wo noch theorieverbiegend debattiert wird, ob sogar Auflösungs- und Strehlverlust durch Obstruktion unterstellt werden kann. Da ist schon eher erwähnenswert, dass bei solchen Größenunterschieden das Öffnungsverhältnis eben nur bei 203 mm verspiegelter Fläche des HS und einer gemessenen Brennweiten von 1200 mm f/6 ist. Mit 195 mm verspiegelter Fläche haben wir denn f/6,15 und auch die Obstrunktion geht in dem Fall mit einem 50 mm Fangspiegel von 24,6 auf 25,6% nach oben. Gewichtung nach eigenem Ermessen. So weit, so gut, dann gibt es ja auch noch unterschiedliche Reflektionsgrade, die da nochmal eine Schippe drauf legen....das wird aber dann endlos, also lasse ich das jetzt dabei bewenden.
Auflösung ist erstrangig an Öffnung gebunden, dann kommt die grundsätzliche Qualität und dann kommt mal gaaaaanz lange gar nichts.
Natürlich vermeide ich zu hohe Obstruktionswerte durch zu große Fangspiegel, aber ich vermeide ebenso mangelnde Ausleuchtung, Öffnungsschwund, den Streulicht schwangern Beitrag einer rauen Fase zur Abblildung und die Wahl eines zu kleinen Fangspiegels.
Selbstverständlich vermeide ich den Kauf von Teleskopen mit dicken Guss- oder Plastikfangspiegelstreben, denn eine gut gebaute, spannbare Spinne mit geraden Armen steift, auch wenn sie sehr dünne Streben hat, den Tubus aus und hält ihn in Form.
Konsequent verzichte ich auch auf die drei bis fünf Klammerbacken mit denen bei vielen Fassungen der Hauptspiegel gehalten wird. Kürzlich sah ich einen 10 Zoll Newton bei dem fünf solcher Gummibacken mit 30 mm Breite jeweils 10 mm auf die die verspiegelte Fläche griffen. Diese Eingriffe und damit auch die resultierenden Beugungserscheinungen, sind bei einem Newton konstruktiv absolut vermeidbar, der Fangspiegel und seine Halterung sind es nicht.
Unvermeidlich hat bei mir eine gebogene Spinne nur die erforderliche Materialstärke, also möglichst wenig Fläche, bei guter Justiersabilität.

